树链刨分学习总结
- 2020 年 7 月 3 日
- 筆記
概念:
对于一棵有根树,每个非叶节点选择至多一个连向孩子的边称为 “实边”(重边) ,这个边集称为这棵树的一个链剖分,不在集合中的边称为“虚边“(轻边)。如图,黑边为重边,白边为轻边。
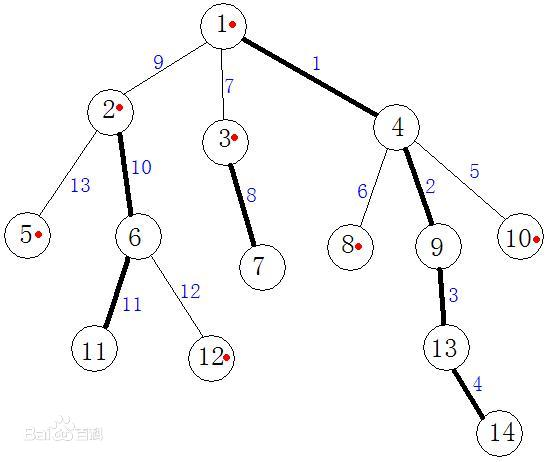
重链:
每个非叶节点向他的节点数最大的子节点连一条重边;
重链求LCA:
如果两个点在同一条链上,则深度小的为答案。否则让较深的点爬到他所在的这条重链的最高点的父亲。
重链DFS序列:
当初始化每个节点的子节点数后(第一次DFS),再进行一次DFS,这一次DFS当递归到某一节点时,给他赋值一个下标,之后先递归他的子节点数最多的子节点,再递归其他子节点,这样就能让任意一条重链对应一个连续的区间。
【NOI2015】软件包管理器(题目):
模板


1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 7 const int N = 200010; 8 9 int n; 10 int tid[N], top[N], pos[N], tidnum; 11 int size1[N], fa[N], dep[N], son[N]; 12 int h[N], nex[N * 2], num[N * 2], dqx; 13 14 struct Node 15 { 16 int l, r, sum, flag; 17 Node() {} 18 }; 19 20 Node tree[N * 4]; 21 22 void add(int a, int b) 23 { 24 num[dqx] = b; 25 nex[dqx] = h[a]; 26 h[a] = dqx++; 27 } 28 29 void dfs1(int u, int father, int depth) 30 { 31 size1[u] = 1; 32 fa[u] = father; 33 dep[u] = depth + 1; 34 for (int i = h[u]; ~i; i = nex[i]) 35 { 36 int j = num[i]; 37 if (j == father) continue; 38 dfs1(j, u, depth + 1); 39 size1[u] += size1[j]; 40 if (!son[u] || size1[j] > size1[son[u]]) son[u] = j; 41 } 42 } 43 44 void dfs2(int u, int tp) 45 { 46 tid[u] = ++tidnum; 47 pos[tid[u]] = u; 48 top[u] = tp; 49 50 if (!son[u]) return; 51 52 dfs2(son[u], tp); 53 for (int i = h[u]; ~i; i = nex[i]) 54 { 55 int j = num[i]; 56 if (j != son[u] && j != fa[u]) 57 { 58 dfs2(j, j); 59 } 60 } 61 } 62 63 void build(int id, int l, int r) 64 { 65 tree[id].l = l; 66 tree[id].r = r; 67 tree[id].sum = 0; 68 tree[id].flag = -1; 69 70 if (l == r) return; 71 int mid = (l + r) >> 1; 72 build(id << 1, l, mid); 73 build(id << 1 | 1, mid + 1, r); 74 } 75 76 void pushdown(int q) 77 { 78 tree[q << 1].sum = (tree[q << 1].r - tree[q << 1].l + 1) * tree[q].flag; 79 tree[q << 1 | 1].sum = (tree[q << 1 | 1].r - tree[q << 1 | 1].l + 1) * tree[q].flag; 80 tree[q << 1].flag = tree[q << 1 | 1].flag = tree[q].flag; 81 tree[q].flag = -1; 82 } 83 84 int get(int q, int l, int r) 85 { 86 if (tree[q].r<l || tree[q].l>r) return 0; 87 if (tree[q].l >= l && tree[q].r <= r) return tree[q].sum; 88 if (~tree[q].flag) pushdown(q); 89 return get(q << 1, l, r) + get(q << 1 | 1, l, r); 90 } 91 92 void update(int q, int l, int r, int v) 93 { 94 if (tree[q].r<l || tree[q].l>r) return; 95 if (tree[q].l >= l && tree[q].r <= r) 96 { 97 tree[q].sum = (tree[q].r - tree[q].l + 1) * v; 98 tree[q].flag = v; 99 return; 100 } 101 102 if (~tree[q].flag) pushdown(q); 103 update(q << 1, l, r, v); 104 update(q << 1 | 1, l, r, v); 105 tree[q].sum = tree[q << 1].sum + tree[q << 1 | 1].sum; 106 return; 107 } 108 109 void change(int a, int b, int v) 110 { 111 while (top[a] != top[b]) 112 { 113 if (dep[a] < dep[b]) swap(a, b); 114 update(1, tid[top[a]], tid[a], v); 115 a = fa[top[a]]; 116 } 117 118 if (dep[a] > dep[b]) swap(a, b); 119 update(1, tid[a], tid[b], v); 120 return; 121 } 122 123 int main() 124 { 125 scanf("%d", &n); 126 127 memset(h, -1, sizeof(h)); 128 for (int i = 2; i <= n; i++) 129 { 130 int a; 131 scanf("%d", &a); 132 a++; 133 add(a, i); 134 } 135 136 dfs1(1, 1, 1); 137 dfs2(1, 1); 138 139 int q; 140 scanf("%d", &q); 141 build(1, 1, tidnum); 142 while (q--) 143 { 144 char s[20]; 145 scanf("%s", s); 146 147 int x; 148 scanf("%d", &x); 149 x++; 150 151 int t1 = tree[1].sum; 152 if (s[0] == 'i') 153 { 154 change(1, x, 1); 155 int t2 = tree[1].sum; 156 printf("%d\n", abs(t1 - t2)); 157 } 158 else 159 { 160 update(1, tid[x], tid[x] + size1[x] - 1, 0); 161 int t2 = tree[1].sum; 162 printf("%d\n", abs(t1 - t2)); 163 } 164 } 165 166 167 }
View Code


