量子纠错码——Clifford group
Clifford code
Clifford group是什么?
简单的公式来表达,就是 \(Cl_{n}=\left\{U: U P_{n} U^{\dagger} \in P_{n}\right\}\) 。
用语言来描述,就是对一个泡利施加一个U操作,然后还是一个泡利。
首先,所有的泡利都属于\(Cl_n\),因为泡利矩阵自己相乘还是泡利。
但也有非泡利的矩阵在这里面,比如H也属于clifford,\(HXH=Z\),$ HZH=X$
另一个例子是 \(S=\sqrt{Z}=\left(\begin{array}{cc}1 & 0 \\ 0 & i\end{array}\right)\)
\(SZS^{\dagger}=ZSS^{\dagger}=Z\)
\(SXS^{\dagger}=iY\)
但是也并非所有的操作都属于\(Cl_n\),比如T门,\(TZT^{\dagger}=ZTT^{\dagger}=ZS \notin P\)
对于单量子比特来说:\(Cl_1=\langle X,Z,H,S\rangle\)
但是我们不仅只有单比特,对于多比特,他不是简单的\(Cl_1^{\otimes n}\) ,因为多比特有纠缠。
比如\(SWAP_{ij}\) ,将第i个和第j个交换一下,这很明显操作完了还是一个泡利,属于\(Cl_n\),\(\operatorname{SWAP}_{i j} X_{i} \operatorname{SWAP}_{i j}^{\dagger}=X_{j}\)
除此之外还有CNOT,CNOT对于原来的泡利在受控比特和控制比特上有所不一样,对X和Z的影响也不一样,其效果如下表:

事实上,我们可以用3个CNOT来构建一个SWAP
所以 \(C l_{n}=\langle H_{i},S_{j},CNOT_{i j}\rangle\)
Clifford group可以做什么?
ok,我们已经知道Clifford的定义了,但是我们为什么要定义一个Clifford group呢?他有什么用?
5 qubit code
定义一组对应五比特编码的stabilizer,\(S=\langle Z X X Z I, I Z X X Z, Z I Z X X, X Z I Z X\rangle\),我们可以很容易的给她加上最后一位变成\(S=\langle Z X X Z I, I Z X X Z, Z I Z X X, X Z I Z X, X X Z I Z\rangle\),多出来的这个就是前面4个的乘积,所以不会影响到最后的结果。
接下来,我们定义 normalizers of S ,也就是\(N(S)\)。
对于\(N(S)\),我们只有一个要求,那就是\(N(S)=\left\{p \in P_{n} | p S p^{\dagger}=S\right\}\)。
对于\(p S p^{\dagger}=S\),我们可以换一种理解方式,即\(pg=gp \forall g \in S\)。
trivial code
我们都知道,编码其实就是将低维的空间映射到高维,那么最为朴实的一种映射就是补零操作,\(V_{S} \in\left\{|0\rangle^{\otimes n-k} \otimes|\Psi\rangle:|\Psi\rangle \in \mathbb{C}^{2^{k}}\right\}\),这就是一个简单的把k比特映射到n比特空间的一种trival code。
这种编码的stabilizer很简单,\(S=\left\langle Z_{1}, Z_{2} \dots . Z_{n-k}\right\rangle\),\(Z_i\)的意思是除了第i个比特是Z其他都是I,这个很好理解,因为前面n-k个比特我们都是\(|0\rangle\),是Z的特征向量。
那这两个编码之间有什么关系吗?
我们可以给出以下声明:
对于任意的stabilizer code,都可以通过unitary的转化和trivial code等价。
而这个unitary就属于我们的Clifford group。
假设我有一组stabilizer \(S\),以及这个\(S\)对应的子空间\(V_S\),那么一定存在一个unitary U 使得 \(USU^{\dagger}=\left\langle Z_{1}, Z_{2} \dots . Z_{n-k}\right\rangle\)
这个时候,我们的子空间\(V_{S}\)就变成了\(V_{USU^{\dagger}}\)
后一句话很好理解,原来这个子空间里的向量为\(|\psi\rangle\),现在这个子空间里的每一个向量就变成了\(U|\psi\rangle\)
\((USU^{\dagger})U|\psi\rangle=US|\psi\rangle=U|\psi\rangle\)
那么前一个为什么会存在这个U呢?
先来论证一下他的可能性,U会改变一些东西,但是有一些不会改变,比如,他不会改变这个的特征值,而正好,他们都是泡利矩阵,特征值都是正负1;又比如,U不会改变他们的对易和反对易,他们正好都是对易的操作。
事实上,对于泡利矩阵来说,只要他们的对易反对易的模式相同,那么我就可以用U对他们进行一个映射。
我们可以换一个视角从向量的角度来看一看这个问题
令\(a,b \in \mathbb{F}^n\),那么\(v=\left(\begin{array}{l}a \\ b\end{array}\right) \in F^{2 n}\)
任意一个Pauli都可以用v来表示\(X^{a} Z^{b}=\sigma^{\left(\begin{array}{c}a \\ b\end{array}\right)}\)
那么Clifford group在做什么?
$U\sigmavU{\dagger} \in P_n $
即,其实就是把\(\sigma^{v_1}\)映射成$\sigma^{v_2} $
\(U\sigma^{v}U^{\dagger}=(-1)^{f(v)}\sigma^{g(v)}\)
我们的下一步就是看这里的函数f(v)和g(v)需要满足哪些条件
这里面一个限制就是U变换不会改变操作本来的对易和反对易。
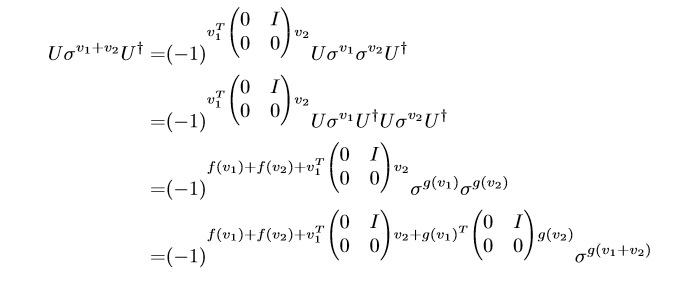
第二个等式是加上了\(U^{\dagger}U\),因为这两个乘积为\(I\)不会有影响
第三个等式是带入公式\(U\sigma^{v}U^{\dagger}=(-1)^{f(v)}\sigma^{g(v)}\)
如果这里面的\(\sigma^v\)就是我们的\(\sigma^{v_1+v_2}\),那么后面我们的到的就是\((-1)^{f(v_1+v_2)}\sigma^{g(v_1+v_2)}\)
即\(g(v_1+v_2)=g(v_1)+g(v_2)\),函数g是一个线性函数
g(v)=Mv
但是也不是所有的M是可行的。
\(\sigma^{v} \sigma^{w} \sigma^{v} \sigma^{w}=(-1)^{v^{T}\Lambda w} I\) 其中\(\lambda=\left(\begin{array}{ll}0 & I \\ 0 & 0\end{array}\right)\)
我们可以先把他展开:
\(U \sigma^{N} U^{\dagger}U \sigma^{W} U^{\dagger}U \sigma^{N} U^{\dagger}U\sigma^{W}U=\sigma^{Mv}\sigma^{Mw}\sigma^{Mv}\sigma^{Mw}\)
这里没有系数,因为两个一模一样的系数乘起来就是1,所以系数可以省略掉。
而如果把\(\sigma^{Mw}\sigma^{Mv}\)交换一下可以变成:
\((-1)^{(Mv)^T\Lambda Mw}I\)
我们可以得出:
\(v^T \Lambda w= v^TM^T \Lambda M w\)
即\(\Lambda=M^T \Lambda M\)
而这个就是M需要满足的条件,属于symplectic group。


