不要小瞧数组
- 2019 年 10 月 3 日
- 筆記
一、简介
本文开始梳理数据结构的内容,从数组开始,逐层深入。
二、java中的数组
在java中,数组是一种效率最高的存储和随机访问对象引用序列的方式。数组是一种线性序列,这使得元素访问非常快速。但是为了这种快速所付出的代价是数组对象的大小被固定,并且是在其整个生命周期中不可被改变,简单的来说可以理解为数组一旦被初始化,则其长度不可被改变。
从上面一段话中我们不难发现几个关键词:效率最高,随机访问,线性序列,长度固定。
从而我们对数组的优缺点就可见一斑:
优点:
随机访问。数组的随机访问速度是O(1)的时间复杂度。效率极高。 缺点:
长度固定。一旦初始化完成,数组的大小被固定。灵活性不足。
上面我们说数组是一种线性序列,如何理解这句话呢?简单来说就是将数据码成一排进行存放。
三、数组的内存分配
int[] a = new int[5];//数组的静态初始化
执行上面这行代码,JVM的内存是如何分布的呢?
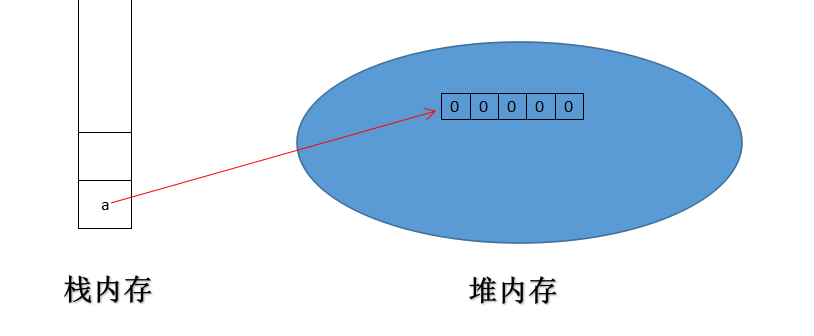
如图所示根据代码的定义,该数组的长度为5,则在栈内存中开辟长度为5的连续内存空间。并且JVM会自动根据类型分配初始值。int 类型的初始值为0。如果类型为Integer,初始值为null(这是java基础内容)。
1 a[0] = 0; 2 a[1] = 1; 3 a[2] = 2; 4 a[3] = 3; 5 a[4] = 4;
如果再执行如上代码,内存分配如下:
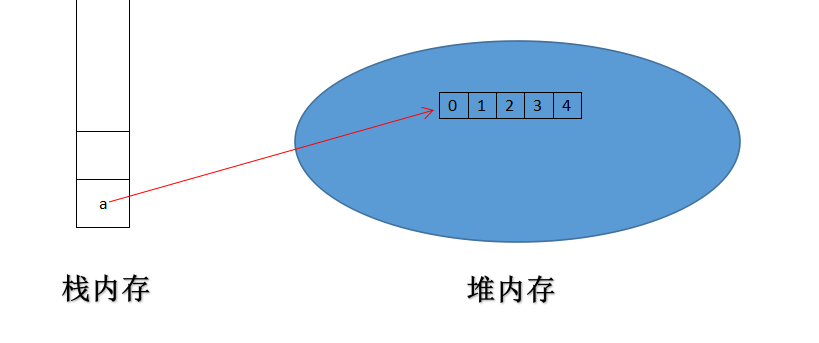
正如以上代码所示,数组的存储效率也是极高的,可根据下标直接将目标元素存放至指定的位置。所以添加元素的时间复杂度也是O(1)级别的。
四、数组的二次封装。
本章我们的重点是封装一个属于自己的数组。对于二次封装的数组我们想要达到的效果如下所示:
1 使用java中的数组作为底层数据结构 2 数组的基本操作:增删改查等 3 使用泛型-增加灵活性 4 动态数组-解决数组最大的痛点
4.1、定义我们的动态数组类
1 /** 2 * 描述:动态数组类 3 * 4 * @Author shf 5 * @Date 2019/7/18 10:48 6 * @Version V1.0 7 **/ 8 public class Array<E> {// 使用泛型 9 private final static int DEFAULT_SIZE = 10;// 默认的数组容量 10 11 private E[] data;// 动态数组的底层容器 12 private int size;// 数组的长度 13 14 /** 15 * 根据传入的 capacity 定义一个指定容量的数组 16 * @param capacity 17 */ 18 public Array(int capacity){ 19 this.data = (E[])new Object[capacity]; 20 this.size = 0; 21 } 22 23 /** 24 * 无参构造方法 - 默认容量为 DEFAULT_SIZE = 10; 25 */ 26 public Array(){ 27 this(DEFAULT_SIZE); 28 } 29 }
TIPS: java中泛型不能直接 new 出来。需要new Object,然后强转为我们的泛型。 如下所示: this.data = (E[])new Object[capacity];
4.2,添加元素
对于我们的数组,我们需要规定数组中的元素都存放在 size – 1的位置。这样做首先我们能根据size参数知道,开辟的数组空间哪些被用了,哪些还没被用。另外一个重要作用就是判断我们的数组是不是已经满了,为后面的动态扩容奠定基础。
4.2.1、 向数组尾部添加元素
最初我们的数组如下图所示:
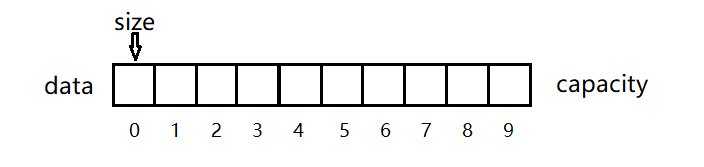
我们在数组的尾部添加一个元素也就是在size处添加一个元素。
代码实现一下:
1 /** 2 * 向数组的尾部 添加 元素 3 * @param e 4 */ 5 public void addLast(int e){ 6 if(size == data.length){ 7 throw new IllegalArgumentException("AddLast failed. Array is full."); 8 } 9 data[size] = e; 10 size ++; 11 }
4.2.2 、向索引 index 处添加元素
如下图所示,如果我们想在 index 为2的位置添加一个元素66。
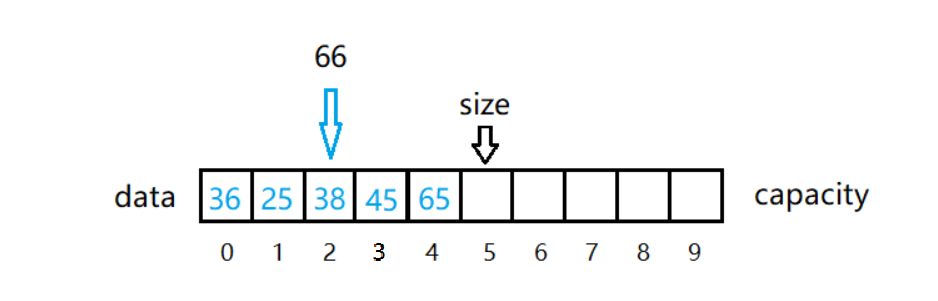
如图中所示,我们想在 index = 2 的位置添加元素,我们需要将 index为2 到尾部的所有元素移动往后移动一个位置。然后将66方法 2索引位置。
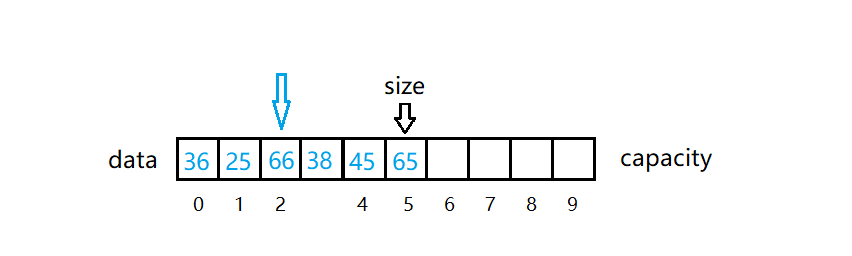
接下来我们用代码实现一下这个过程。
1 /** 2 * 在 index 的位置插入一个新元素e 3 * @param index 4 * @param e 5 */ 6 public void add(int index, int e){ 7 8 if(size == data.length) 9 throw new IllegalArgumentException("Add failed. Array is full."); 10 11 if(index < 0 || index > size) 12 throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size."); 13 14 for(int i = size - 1; i >= index ; i --) 15 data[i + 1] = data[i]; 16 17 data[index] = e; 18 19 size ++; 20 }
我们发现有了这个方法,4.2.1中的向数组尾部添加元素就可以直接调用该方法,并且对于向数组头添加元素也是显而易见了。
1 /** 2 * 向数组 尾部 添加元素 3 * @param e 4 */ 5 public void addLast(E e){ 6 this.add(this.size, e); 7 } 8 9 /** 10 * 向数组 头部 添加元素 11 * @param e 12 */ 13 public void addFirst(E e){ 14 this.add(0, e); 15 }
4.3、删除
删除指定位置的元素。假设我们删除 index = 2位置的元素66。
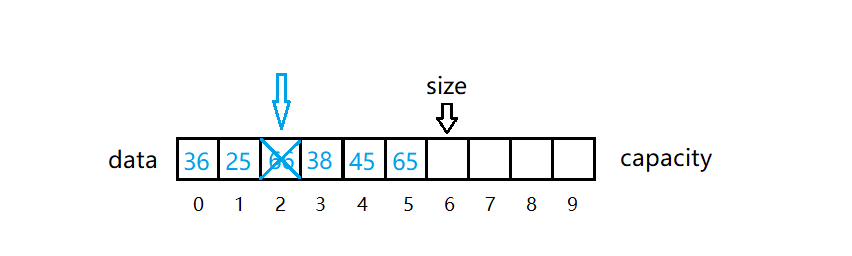
如上图所示,我只需要将索引 2 以后的元素向前移动一个位置,并重新维护一下size即可。
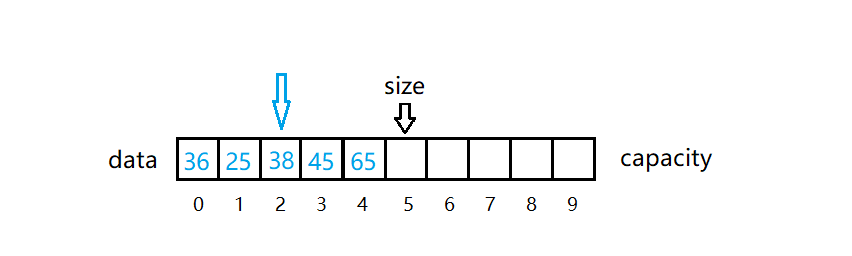
代码实现一下上面过程:
1 /** 2 * 删除指定位置上的元素 3 * @param index 4 * @return 返回删除的元素 5 */ 6 public int remove(int index){ 7 if(index < 0 || index >= size) 8 throw new IllegalArgumentException("Remove failed. Index is illegal."); 9 10 int ret = data[index]; 11 for(int i = index + 1 ; i < size ; i ++) 12 data[i - 1] = data[i]; 13 size --; 14 return ret; 15 }
有了上面的方法,对于删除数组 头 或者 尾 部的元素就好办了
1 /** 2 * 删除第一个元素 3 * @return 4 */ 5 public E removeFirst(){ 6 return this.remove(0); 7 } 8 9 /** 10 * 从数组中删除最后一个元素 11 * @return 12 */ 13 public E removeLast(){ 14 return this.remove(this.size - 1); 15 }
4.4、查找,修改,搜索等操作
这些操作都是不改变数组长度的操作,逻辑相对来说就很简单了。
1 /** 2 * 获取 index 索引位置的元素 3 * @param index 4 * @return 5 */ 6 public E get(int index){ 7 if(index < 0 || index >= size){ 8 throw new IllegalArgumentException("获取失败,Index 参数不合法"); 9 } 10 return this.data[index]; 11 } 12 13 /** 14 * 获取第一个 15 * @return 16 */ 17 public E getFirst(){ 18 return get(0); 19 } 20 21 /** 22 * 获取最后一个 23 * @return 24 */ 25 public E getLast(){ 26 return get(this.size - 1); 27 } 28 29 /** 30 * 修改 index 元素位置的元素为e 31 * @param index 32 * @param e 33 */ 34 public void set(int index, E e){ 35 if(index < 0 || index >= size){ 36 throw new IllegalArgumentException("获取失败,Index 参数不合法"); 37 } 38 this.data[index] = e; 39 } 40 41 /** 42 * 查找数组中是否有元素 e 43 * @param e 44 * @return 45 */ 46 public Boolean contains(E e){ 47 for (int i = 0; i< size; i++){ 48 if(this.data[i].equals(e)){ 49 return true; 50 } 51 } 52 return false; 53 } 54 55 /** 56 * 查找数组中元素e所在的索引,如果不存在元素e,则返回-1 57 * @param e 58 * @return 59 */ 60 public int find(E e){ 61 for(int i=0; i< this.size; i++){ 62 if(this.data[i].equals(e)){ 63 return i; 64 } 65 } 66 return -1; 67 }
4.5、resize操作
既然是动态数组,resize操作就是我们的重中之重了。
4.5.1、扩容
扩容是添加操作触发的。
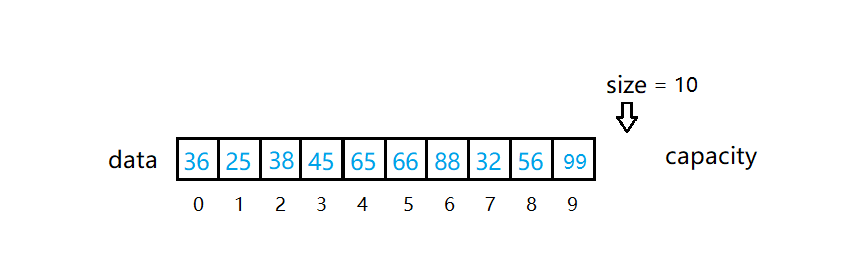
如图所示,如果我们继续往数组中添加元素100,这时我们就需要进行扩容了。我们将原来的容量 capacity 扩充为原来的两倍,然后再进行添加。即:capacity * 2 = 20;(以capacity默认为10为例)
扩容的临界值:size == capacity时继续添加。
首先将容量扩充为原来的2倍:
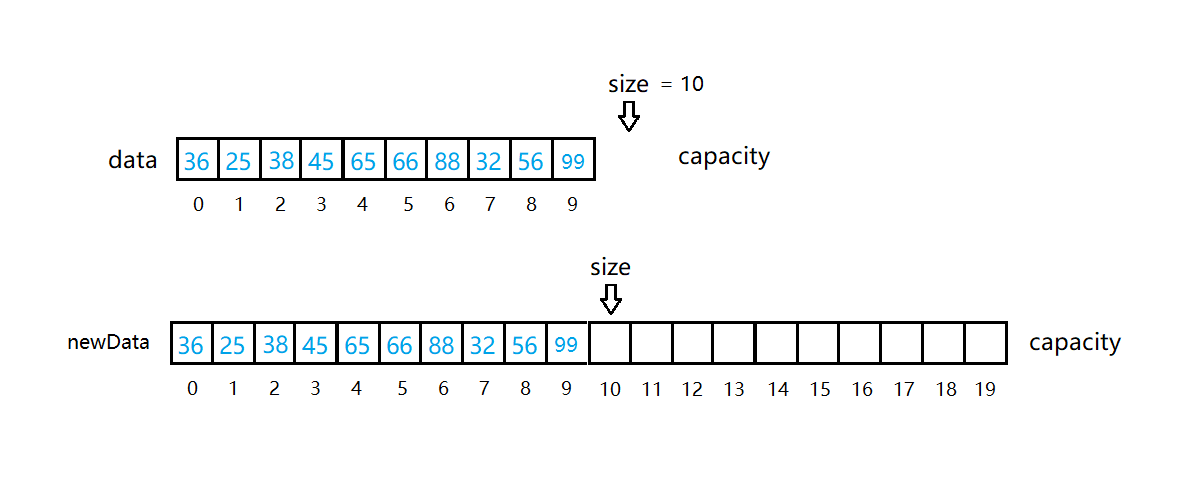
然后添加元素100
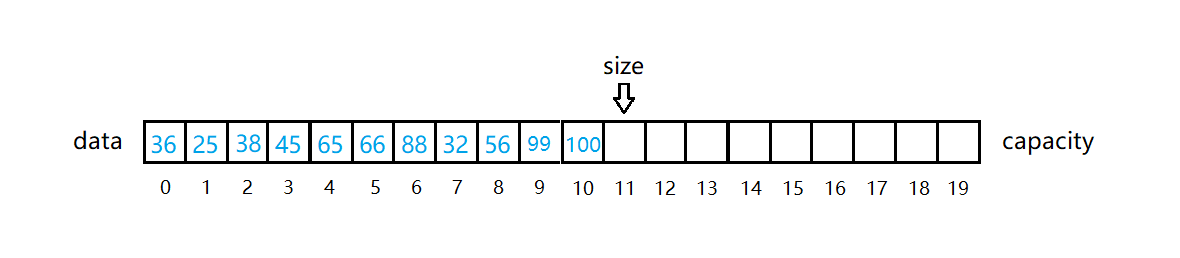
代码上,对于add方法我们要做如下改变:
1 /** 2 * 在 index 的位置插入一个新元素e 3 * @param index 4 * @param e 5 */ 6 public void add(int index, E e){ 7 if(index < 0 || this.size < index){ 8 throw new IllegalArgumentException("添加失败,要求参数 index >= 0 并且 index <= size"); 9 } 10 if(size == data.length){ 11 this.resize(2 * data.length);//扩容 12 } 13 for (int i = size - 1; i >= index; i--) { 14 data[i + 1] = data[i]; 15 } 16 data[index] = e; 17 size ++; 18 }
在添加元素之前,我们进行判断size == data.length(n*capacity,n代表扩容次数,如果我们用capacity,需要维护一个n,或者每次操作都要维护capacity,我们直接用data.length判断)
对于resize方法,逻辑就很简单了。新创建一个容量为newCapacity的数组,将原数组中的元素拷贝到新数组即可。从这可以发现,每次resize操作由于需要有一个copy操作,时间复杂度为O(n)。
1 /** 2 * 将数组容量调整为 newCapacity 大小 3 * @param newCapacity 4 */ 5 public void resize(int newCapacity){ 6 E[] newData = (E[]) new Object[newCapacity]; 7 for (int i = 0; i< this.size; i++){ 8 newData[i] = this.data[i]; 9 } 10 this.data = newData; 11 }
4.5.2、缩容
缩容在删除操作中触发。
接着上面的步骤,如果我们想删除元素100,该怎么做?
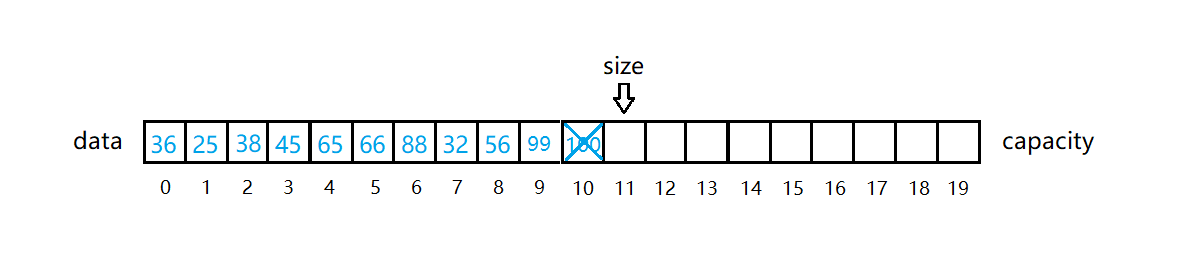
删除100元素后才达到resize的临界值 size == 1/2*capacity。所以缩容的时机为删除元素后当 size == 1/2的capacity时。

进行缩容操作:
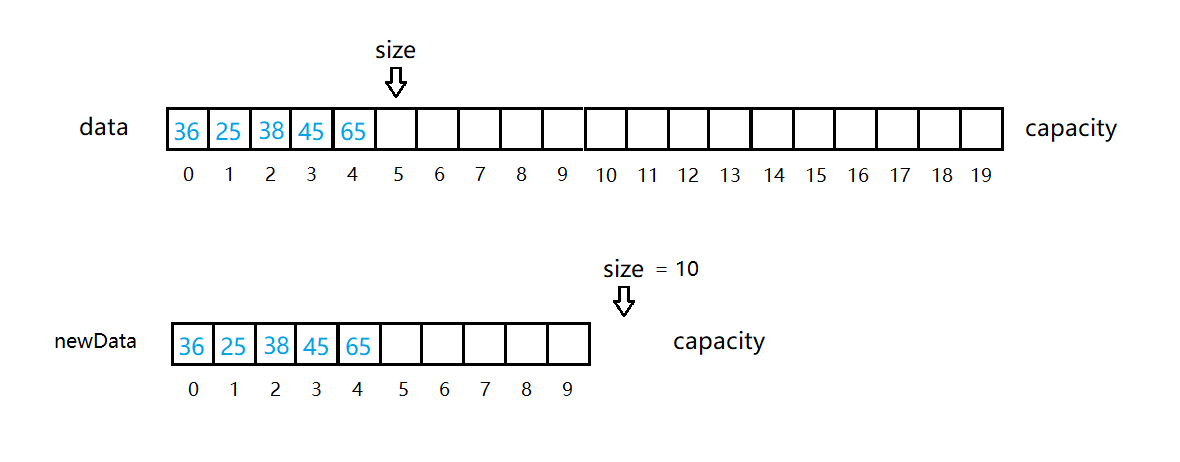
如上图所示,这时size == 1/2*capacity,已经到了我们缩容的时机。
我们考虑一个问题,假如删除了元素100后,将容量缩为原来的1/2 = 10,如果这时,我又添加元素,是不是又得进行扩容,再删除一个元素,又得缩容。。。
这样频繁的进行扩容,缩容是不是很耗时?这种频繁的进行缩容和扩容会引起复杂度震荡。那我们该如何防止复杂度的震荡呢?很简单,假如我们为扩容–缩容取一个过渡带,即当容量为原来的1/4时再进行缩容是不是就可以避免这种问题了?答案,是的。
代码实现的两个重点:1,防止复杂度震荡。2,缩容发生在 删除一个元素后size == 当前容量的1/4时。
1 /** 2 * 删除指定位置上的元素 3 * @param index 4 * @return 5 */ 6 public E remove(int index){ 7 if(index < 0 || this.size <= index){ 8 throw new IllegalArgumentException("删除失败,Index 参数不合法"); 9 } 10 E ret = this.data[index]; 11 for(int i=index+1; i< this.size; i++){ 12 data[i-1] = data[i]; 13 } 14 size --; 15 this.data[this.size] = null; 16 if(size == this.data.length / 4 && this.data.length / 2 != 0){//防止复杂度的震荡,当size == 1/4capacity时。 17 this.resize(this.data.length / 2); 18 } 19 return ret; 20 }
五、动态数组的时间复杂度分析
5.1、增
addFirst(e) O(n)
addLast(e) O(1)
add(index, e) O(1)-O(n) = O(n)
所以add整体的复杂度最坏情况为O(n)。
5.2、删
removeLast(e) O(1)
removeFirst(e) O(n)
remove(index, e) O(1)-O(n) = O(n)
所以remove整体的复杂度最坏情况为O(n)。
5.3、resize的均摊复杂度
对于resize来说,每次进行一次resize,时间复杂度是O(n)。但是对于resize我们仅仅通过resize操作来界定其时间复杂度合理吗?考虑一个问题,resize操作是每次add或者remove操作都会触发的吗?答案肯定不是的。因为假设当前数组的容量为10,每次使用addLast添加一个元素,需要进行11次的添加操作,才会发生一次resize,一次resize对应10次的元素移动过程。也就是直到resize完成,一共进行了21次操作。假设capacity=n,addLast = n+1,触发resize共进行了2n+1次操作,所以对于addLast操作来说每一次操作,需要进行2次基本操作。
这样均摊计算,addLast的均摊复杂度就是O(1)级别的。均摊复杂度有时比计算最坏的情况更有意义,因为对坏的情况不是每次都发生的。
同理对于removeLast操作来说,均摊复杂度也是O(1)级别的。
5.4、resize操作的复杂度震荡
对于addLast和removeLast操作而言,时间复杂度都是O(1)级别的,但是当我们对这两个操作整体来看,在极端情况下可能会发生的有趣的案例
假设对于添加操作当数组size == capacity 扩容为当前容量的2倍。对于removeLast,达到当前数组容量的1/2,进行缩容,缩为当前容量的1/2。
当前数组的容量为10,这时反复进行addLast和removeLast操作。我们会发现有意思的情况就是对于两个复杂度为O(1)级别的操作,由于每次都触发resize操作,时间复杂度每次都是最坏的情况O(n)。这种由于某种操作造成的复杂度不断变化的情况称为-复杂度的震荡。
如何解决复杂度的震荡呢?上面我们也提到过,就是添加一个缓冲带,减少这种情况的发生。那就是当容量变为原来的1/4时进行缩容。所以对于addLast和removeLast的操作,中间间隔1/4容量的操作才会发生复杂度的震荡。这样我们就有效的减少了复杂度的震荡。
看到这里如果你发现我们手写的动态数组跟java中的ArrayList很相似的话,说明你对ArrayList的了解还是很不错的。
参考文献:
《玩转数据结构-从入门到进阶-刘宇波》
《数据结构与算法分析-Java语言描述》
如有错误的地方还请留言指正。
原创不易,转载请注明原文地址:https://www.cnblogs.com/hello-shf/p/11299383.html
