【数据结构】带权并查集

• 2021 年 2 月 17 日
• 筆記
• 算法笔记

目录

• 简介
• 详细介绍
• 例题

简介

顾名思义，就是在维护集合关系的树中添加边权的并查集，这样做可以维护更多的信息。

引入题目：//www.luogu.com.cn/problem/P2024
比如这道题，如果使用普通的并查集则无法处理，因为普通的并查集只能够刻画两个物品是否属于同一个集合。因此这时候就要使用能够记录更多信息的带权并查集。

在阅读前，需要先掌握并查集的知识。

详细介绍

结合题目讲解：//www.luogu.com.cn/problem/P2024

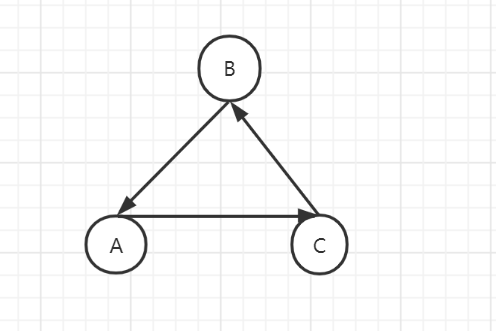
对于一个物种（一类动物），如果存在它吃另一个物种的关系，则让它的度数比另一个物种多 \(1\) 。更严格地说，我们记该物种为 a （并非题意中的A），另一个物种是 b，它们对应的度数为d[]，那么有 \(d[a]=d[b]+1\) 。如图：

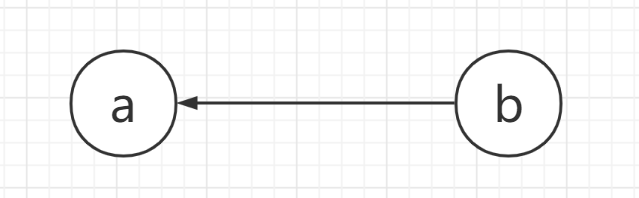
那么有了这样的规定，便有如下性质：

• d[a]%3==d[b]%3 时，a，b是同一个物种。（操作1）
• ((d[a]-d[b])%3+3)%3==1 时，存在a吃b的关系。（这里多次取模是为了保证左边的值只可能为 \(0,1,2\) ）（操作2）

从上面的性质可以看出，两个物种的关系与它们的模数（这题是 \(mod3\) ）余多少关系密切相关，因此接下来我们也会着重考察两个数之间的这种关系。

利用度数以及并查集，即可将各种动物之间的关系刻画清楚：

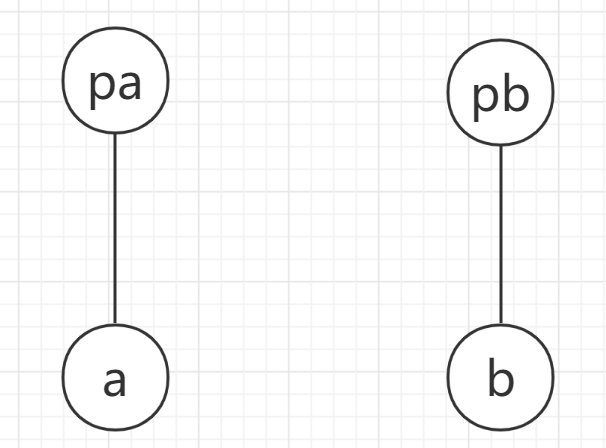
这里依然对a，b进行讨论，为了方便，我们记a的祖宗（根节点）为pa，b的祖宗（根节点）为pb。

• 若pa，pb不在同一个集合中：
  就进行并查集的合并操作，让f[pa]=pb。可以看出，在合并的时候，仍然作为根节点的pb的度数还是 \(0\)，但是pa的度数需要作出调整，才能够保证结点之间关系的正确。
  ① 如果a和b是同一个物种（操作1）：则有 d[pa]+d[a]=d[b]
  ② 如果a吃b（操作2）：则有 d[pa]+d[a]-d[b]=1（当然，右式等于 \(4,7,10\) 这样的数也是可以的，我们只需找到 \(mod 3余1\)的数 ）
  

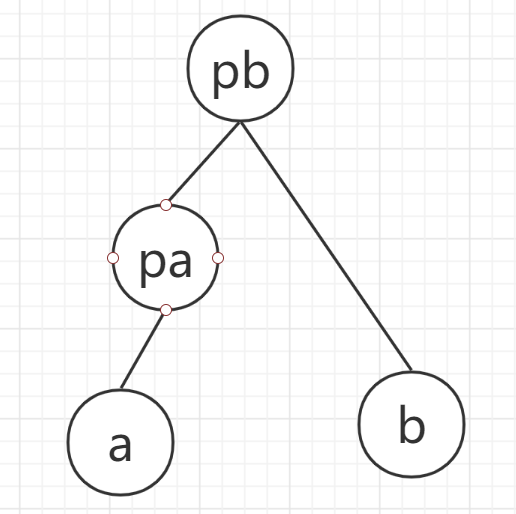
• 若pa，pb在同一个集合中：
  类似于上面的讨论，
  ① 如果a和b是同一个物种（操作1）：如果 ((d[a]-d[b])%3+3)%3!=0，则矛盾，这句话便是谎言。
  ② 如果a吃b（操作2）：如果 ((d[a]-d[b])%3+3)%3!=1，则矛盾，这句话便是谎言。

综上，我们的讨论将所有情况覆盖了。

路径压缩：
根据并查集的性质，如果不进行路径压缩，时间复杂度将会退化到 \(O(N)\) 。因此带权并查集也要进行路径压缩，那么主要问题就是解决如何维护d[]（度数）的问题：
概括地说，就是在查询到某个点的时候，在搜索它的祖宗时递归地求出路上所有结点的度数，那么它的度数就是d[x]+=d[f[x]]。

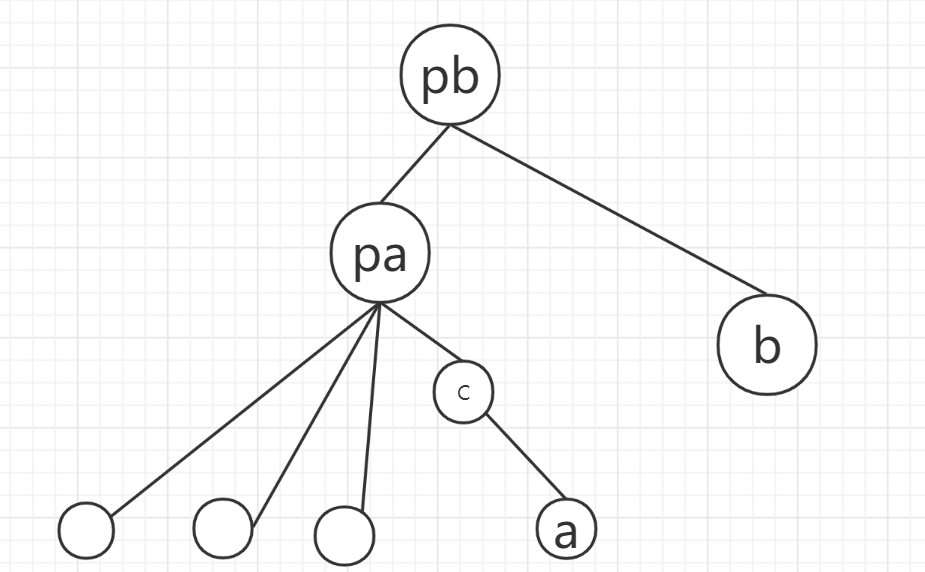
如上图，pa在一次操作中并入了pb。
而在另一次操作中，对a的进行了查询（求祖宗），便有如下路径压缩的并更新d[]的过程：
递归地找出祖宗pb。
pa的祖宗就是pb，度数在合并的时候已经求出来了，所以更新 \(0\)。
c的父亲节点是pa，合并的时候并没有更新（因此记录的是距离pa的度数），度数需要加上 \(d[pa]\)，然后进行路径压缩。

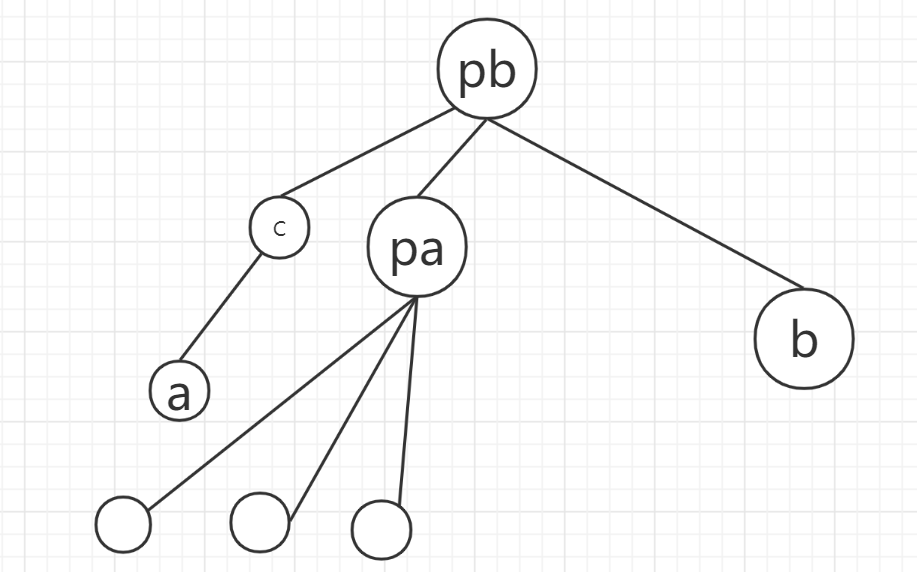
a的父亲节点是c，在上一步更新了，所以度数加上 \(d[c]\) 即可，类似的，进行路径压缩。

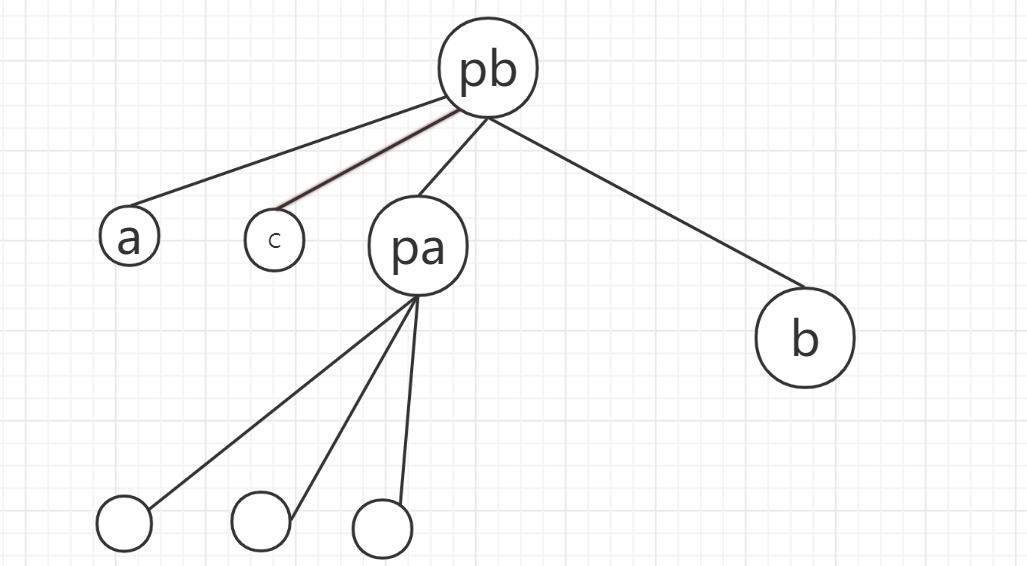
（这里可能有点难理解，不过只要记住：所谓的d[x]指的是节点x相对于它父节点的度数即可）

不理解的地方可以结合代码理解

放上代码：（很短的）

#include<bits/stdc++.h>
using namespace std;

const int N=5e4+5;

int f[N],d[N];

int find(int x){
    if(x!=f[x]){
        int root=find(f[x]);
        d[x]+=d[f[x]];
        f[x]=root;
    }   
    return f[x];
}

int main(){
    int n,m;
    cin>>n>>m;
    
    for(int i=1;i<N;i++) f[i]=i;
    
    int cnt=0;
    while(m--){
        int op,a,b;
        cin>>op>>a>>b;
        
        //2,3 judge
        if(a>n || b>n){
            cnt++;
            continue;
        }
        if(a==b && op==2){
            cnt++;
            continue;
        }
        
        int pa=find(a),pb=find(b);
        
        int t= op==2;
        if(pa==pb){
            if(((d[a]-d[b])%3+3)%3!=t) cnt++;
        }else{
            f[pa]=pb;
            d[pa]=t+d[b]-d[a];
        }
    }
    
    cout<<cnt<<endl;
    
    return 0;
}

例题

//www.acwing.com/problem/content/241/
分析：思路完全类似于食物链那题。

//init
for(int i=1;i<N;i++) f[i]=i;

int ans=m;
for(int i=1;i<=m;i++){
    int a,b;
    string op;
    
    cin>>a>>b>>op;
    a=get(a-1); b=get(b);
    
    int t= op=="odd";
    
    int pa=find(a),pb=find(b);
    
    if(pa==pb){
        if(abs(d[a]-d[b])!=t){
            ans=i-1;
            break;
        }
    }else{
        //merge
        f[pa]=pb;
        d[pa]=d[a]^d[b]^t;
    }
}

cout<<ans<<endl;

return 0;