机器学习入门：极度舒适的GBDT原理拆解

2020 年 7 月 4 日
筆記
Python, 机器学习

机器学习入门：极度舒适的GBDT拆解

本文旨用小例子+可视化的方式拆解GBDT原理中的每个步骤，使大家可以彻底理解GBDT

Boosting→Gradient Boosting

Boosting是集成学习的一种基分类器（弱分类器）生成方式，核心思想是通过迭代生成了一系列的学习器，给误差率低的学习器高权重，给误差率高的学习器低权重，结合弱学习器和对应的权重，生成强学习器。

Boosting算法要涉及到两个部分，加法模型和前向分步算法。
加法模型就是说强分类器由一系列弱分类器线性相加而成。一般组合形式如下：
$$F_M(x;P)=\sum_{m=1}^n\beta_mh(x;a_m)$$
其中，$h(x;a_m)$就是一个个的弱分类器，$a_m$是弱分类器学习到的最优参数，$β_m$就是弱学习在强分类器中所占比重，P是所有$α_m$和$β_m$的组合。这些弱分类器线性相加组成强分类器。

前向分步就是说在训练过程中，下一轮迭代产生的分类器是在上一轮的基础上训练得来的。也就是可以写成这样的形式：
$$F_m (x)=F_{m-1}(x)+ \beta_mh_m (x;a_m)$$

Gradient Boosting = Gradient Descent + Boosting

Boosting 算法（以AdaBoost为代表）用错分数据点来识别问题，通过调整错分数据点的权重来改进模型。Gradient Boosting通过负梯度来识别问题，通过计算负梯度来改进模型。

Gradient Boosting每次迭代的目标是为了减少上一次的残差，在残差减少的梯度(Gradient)方向上建立一个新的模型，每个新的模型的建立是使之前模型的残差往梯度方向减少。

第t轮的第i个样本的损失函数的负梯度为：
$$
\large {r_{mi}} = -\left[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)} \right]{f(x)=f{m-1}(x)}
$$

此时不同的损失函数将会得到不同的负梯度，如果选择平方损失
$L(y_i,f(x_i)) = \frac{1}{2}(y_i – f(x_i))^2$

负梯度为$r_{mi} = y_i – f(x_i)$

此时我们发现GBDT的负梯度就是残差，所以说对于回归问题，我们要拟合的就是残差。

GBDT回归算法

输入是训练集样本$T={(x_,y_1),(x_2,y_2), …(x_m,y_m)}$，最大迭代次数T, 损失函数L。
输出是强学习器$f(x)$

初始化弱学习器
对迭代轮数t=1,2,…T有：
$f_0(x) = \underbrace{arg; min}{c}\sum\limits{i=1}^{m}L(y_i, c)$

a)对样本$i=1,2，…m$，计算负梯度
$$r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]{f(x) = f{t-1};;(x)}$$
b)利用$(x_i,r_{ti});; (i=1,2,..m)$, 拟合一颗CART回归树,得到第t颗回归树，其对应的叶子节点区域为$R_{tj}, j =1,2,…, J$。其中J为回归树t的叶子节点的个数。

c) 对叶子区域$j =1,2,..J$,计算最佳拟合值
$$c_{tj} = \underbrace{arg; min}{c}\sum\limits{x_i \in R_{tj}} L(y_i,f_{t-1}(x_i) +c)$$
d)更新强学习器
$$f_{t}(x) = f_{t-1}(x) + \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj})$$
3) 得到强学习器f(x)的表达式
$$f(x) = f_T(x) =f_0(x) + \sum\limits_{t=1}^{{T}\sum\limits_{j=1}}{J}c_{tj}I(x \in R_{tj})$$

二元GBDT分类算法

对于二元GBDT，如果用类似于逻辑回归的对数似然损失函数，则损失函数为：
$L(y, f(x)) = log(1+ exp(-yf(x)))$
其中y∈{?1,+1}。则此时的负梯度误差为
$$r_{ti} = -\bigg[\frac{\partial L(y, f(x_i)))}{\partial f(x_i)}\bigg]{f(x) = f{t-1};; (x)} = y_i/(1+exp(y_if(x_i)))$$
　　　　对于生成的决策树，我们各个叶子节点的最佳负梯度拟合值为
$$c_{tj} = \underbrace{arg; min}{c}\sum\limits{x_i \in R_{tj}} log(1+exp(-y_i(f_{t-1}(x_i) +c)))$$
　　　　由于上式比较难优化，我们一般使用近似值代替
$$c_{tj} = \sum\limits_{x_i \in R_{tj}}r_{ti}\bigg / \sum\limits_{x_i \in R_{tj}}|r_{ti}|(1-|r_{ti}|)$$
除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索，二元GBDT分类和GBDT回归算法过程相同。

小例子+可视化理解GBDT

上面对原理进行了分析之后，大致对GBDT有了一定的认识，为了更加形象的解释GBDT的内部执行过程，这里引用《统计学习方法》中adaboost一节中的案例数据来进行进一步分析。强烈建议大家对比学习，看一下Adaboost和 GBDT 的区别和联系。
数据集如下：

采用GBDT进行训练，为了方便，我们采用MSE作为损失函数，并且将树的深度设为1，决策树个数设为5，其他参数使用默认值

import numpy as np
import pandas as pd
from sklearn import tree
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split 

X = np.arange(1,11)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])
display(X,y)

gbdt = GradientBoostingRegressor(n_estimators=5,max_depth=1)
gbdt.fit(X.reshape(-1,1),y)

其中GradientBoostingRegressor主要参数如下

GradientBoostingRegressor(alpha=0.9, criterion='friedman_mse', init=None,
                          learning_rate=0.1, loss='ls', max_depth=1,
                          max_features=None, max_leaf_nodes=None,
                          min_impurity_decrease=0.0, min_impurity_split=None,
                          min_samples_leaf=1, min_samples_split=2,
                          min_weight_fraction_leaf=0.0, n_estimators=5,
                          n_iter_no_change=None, presort='auto',
                          random_state=None, subsample=1.0, tol=0.0001,
                          validation_fraction=0.1, verbose=0, warm_start=False)

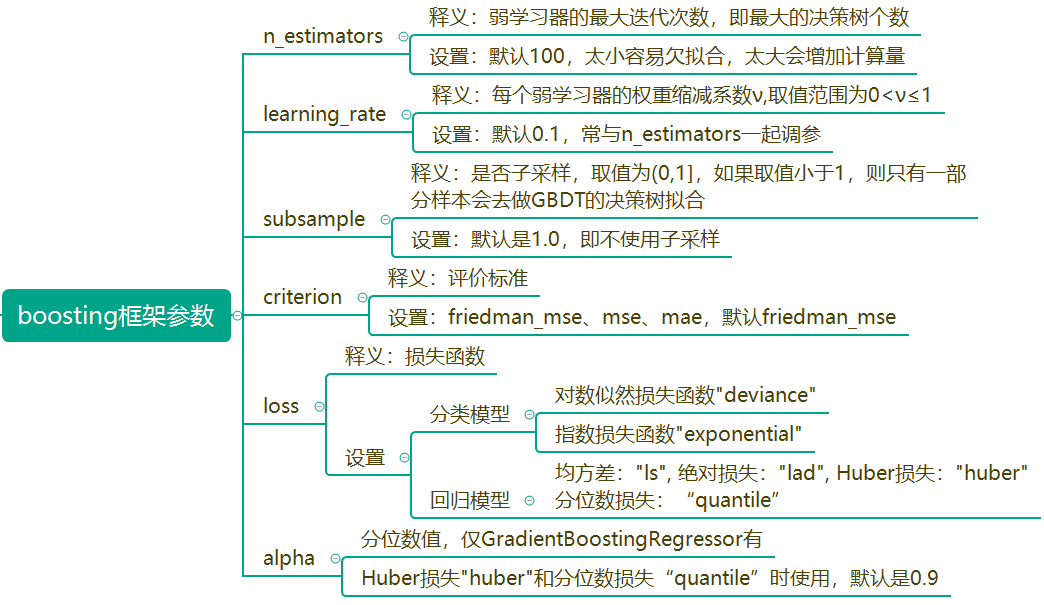
其他参数为决策树参数，大家应该已经很熟悉了，不再赘述。

下面我们根据GBDT回归算法原理，开始分步硬核拆解：

第一步：根据初始化公式
$f_0(x) = \underbrace{arg; min}{c}\sum\limits{i=1}^{m}L(y_i, c)$
可以计算出$F_{0}(x)=7.307$（本例中，恰好为yi均值）

第二步：计算损失函数的负梯度值:
$$r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]{f(x) = f{t-1};; (x)}$$
由于是MSE损失，上式等于$\hat{y}i = y_i – F{m-1}(x_i)$，结果如下：

#计算残差
y - y.mean()
[out]:
array([-1.747, -1.607, -1.397, -0.907, -0.507, -0.257,  1.593,  1.393,
        1.693,  1.743])

第三步：对上面残差拟合第一棵树
根据所给的数据，可以考虑的切分点为1.5、2.5、3.5、4.5、5.5、6.5、7.5、8.5、9.5分别计算$y_i – F_{0}(x_i)$的值，并计算出切分后的左右两侧加和MSE最小的切分，最后得到的是6.5

找到最佳的切分点之后，我们可以得到各个叶子节点区域，并计算出$R_{jm}$和$\gamma_{jm}$.此时，$R_{11}$为$x$小于6.5的数据，$R_{21}$为x大于6.5的数据。同时，

$$r_{11} = \frac{1}{6} \sum_{x_i \in R_{11}} y_{i}=-1.0703$$

$$r_{21} = \frac{1}{4} \sum_{x_i \in R_{21}} y_{i}=1.6055$$

print((y - y.mean())[:6].mean(),
(y - y.mean())[6:10].mean())
[out]:-1.07 1.605
#计算mse
print(
((y - y.mean())**2).mean(),
((y[:6] - y[:6].mean())**2).mean(),
((y[6:10] - y[6:10].mean())**2).mean())
[out]
1.911421 0.309689 0.0179686

第一棵树的可视化

tree.plot_tree(gbdt[0,0],filled=True)

最后：更新$F_{1}(x_i)$的值
$F_1(x_i)=F_{0}(x_i)+ \rho_m \sum^2_{j=1} \gamma_{j1} I(x_i \in R_{j1})$，其中$\rho_m$为学习率，或称shrinkage，目的是防止预测结果发生过拟合，默认值是0.1。

至此第一轮迭代完成，后面的迭代方式与上面一样，
本例中我们生成了5棵树，大家可以用tree.plot_tree可视化其他树

课后作业，大家可以思考一下，第二棵树中的value是如何计算出来的？其实很简单哈????

迭代$m$次后，第$m$次的$F_{m}(x)$即为最终的预测结果。

Tags: Python 机器学习