面试中很值得聊的二叉树遍历方法——Morris遍历

2020 年 5 月 27 日
筆記
数据结构和算法

Morri遍历

通过利用空闲指针的方式，来节省空间。时间复杂度O(N)，额外空间复杂度O(1)。普通的非递归和递归方法的额外空间和树的高度有关，递归的过程涉及到系统压栈，非递归需要自己申请栈空间，都具有O(N)的额外空间复杂度。

Morri遍历的原则:

1. 假设当前节点为cur，

2. 如果cur没有左孩子，cur向右移动，cur = cur.right

3. 如果cur有左孩子，找到左子树上最右的节点mostRight

　　3.1 如果mostRight.right == null，令mostRight.right = cur，cur向左移动，cur = cur.left

　　3.2 如果mostRight.right == cur，令mostRight.right = null，cur向右移动，cur = cur.right

4. 如果cur == null 停止遍历

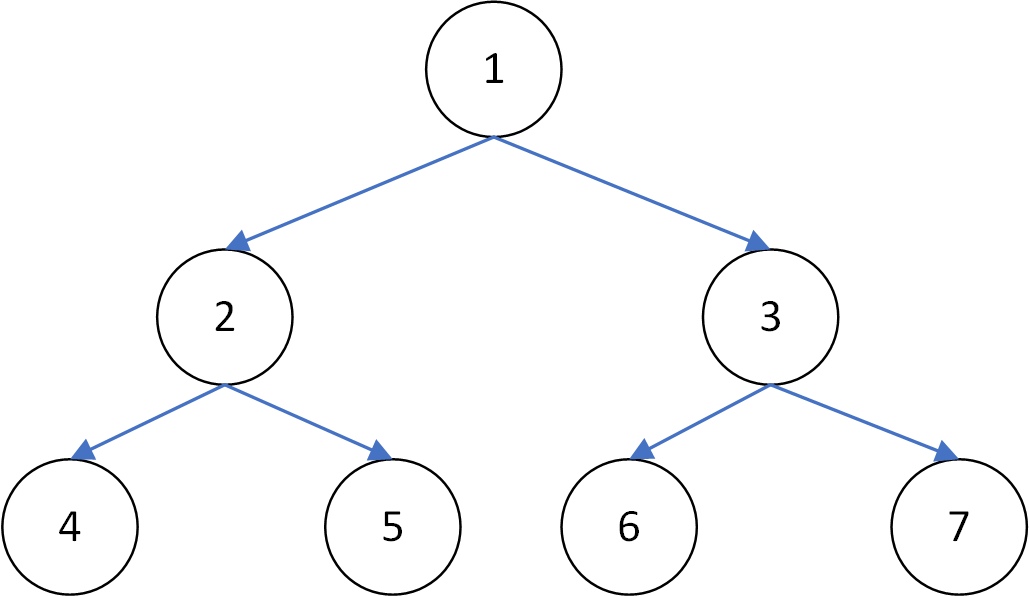
Morris：1242513637

 1     public static void morris(TreeNode head){
 2         if(head == null) return;
 3         TreeNode cur = head;
 4         TreeNode mostRight = null;
 5         while(cur != null){//cur为空遍历停止【4】
 6             mostRight = cur.left;//是cur左子树上最右的节点
 7             if(mostRight != null){//有左子树【3】
 8                 while(mostRight.right != null && mostRight != cur){//mostRight!=cur不加就会绕环循环
 9                     mostRight = mostRight.right;//找最右节点【3】
10                 }
11                 if(mostRight.right == null){//第一次来到cur【3.1】
12                     mostRight.right = cur;
13                     cur = cur.left;
14                     continue;//执行循环
15                 }else {//mostRight.right = cur第二次来到cur【3.2】
16                     mostRight.right = null;
17                 }
18             }
19             cur = cur.right;//没有左子树【2】
20 
21         }
22     }

所有节点遍历左子树右边界的时间总代价O(N)

基于Morris的先中后序遍历

如果cur有左子树一定能遍历2次，没有左子树只能遍历一次。

先序遍历

Morris：1242513637

Morris先序：1245367

基于Morris的先序遍历，如果一个节点可以到达两次则打印第一次，如果只能到达一次直接打印。

 1     public static void morrisPre(TreeNode head){
 2         if(head == null) return;
 3         TreeNode cur = head;
 4         TreeNode mostRight = null;
 5         while(cur != null){//有左子树
 6             mostRight = cur.left;
 7             if(mostRight != null){
 8                 while(mostRight.right != null && mostRight != cur){
 9                     mostRight = mostRight.right;
10                 }
11                 if(mostRight.right == null){//第一次来到左子树
12                     System.out.println(cur.val);//打印
13                     mostRight.right = cur;
14                     cur = cur.left;
15                     continue;
16                 }else {
17                     mostRight.right = null;
18                 }
19             }else{
20                 System.out.println(cur.val);//没有左子树 只会遍历一次
21             }
22             cur = cur.right;
23         }
24     }

中序遍历

Morris：1242513637

Morris中序：4251637

基于Morris的中序遍历，如果一个节点可以到达两次则打印第二次，如果只能到达一次直接打印。

 1     public static void morrisIn(TreeNode head) {
 2         if(head == null) return;
 3         TreeNode cur = head;
 4         TreeNode mostRight = null;
 5         while(cur != null){
 6             mostRight = cur.left;
 7             if(mostRight != null){
 8                 while(mostRight.right != null && mostRight != cur){
 9                     mostRight = mostRight.right;
10                 }
11                 if(mostRight.right == null){
12                     mostRight.right = cur;
13                     cur = cur.left;
14                     continue;
15                 }else {
16                     mostRight.right = null;
17                 }
18             }
19             //没有左树跳过if直接打印，有左树第二次来到cur退出循环打印
20             System.out.println(cur.val);
21             cur = cur.right;
22         }
23     }

后序遍历

Morris：1242513637

Morris先序：4526731

基于Morris的后序遍历，如果一个节点可以到达两次则第二次到达时逆序打印左树的右边界，单独逆序打印整棵树的右边界。

（1）逆序右边界（等同于单链表的逆序）

 1       public static TreeNode reverseEdge(TreeNode from) {
 2         TreeNode pre = null;
 3         TreeNode next = null;
 4         while(from != null){
 5             next = from.right;
 6             from.right = pre;
 7             pre = from;
 8             from = next;
 9         }
10         return pre;
11     }

（2）逆序打印以head为头节点的右边界。

1     public static void printRightEdge(TreeNode head) {
2         TreeNode tail = reverseEdge(head);//逆转右边界
3         TreeNode cur = tail;
4         while(cur != null){
5             System.out.println(cur.val + " ");
6             cur = cur.right;
7         }
8         reverseEdge(tail);//逆转回去 恢复原树
9     }

（3）在Morris遍历中按时机打印。

 1     public static void morrisPost(TreeNode head){
 2         if(head == null) return;
 3         TreeNode cur = head;
 4         TreeNode mostRight = null;
 5         while(cur != null){
 6             mostRight = cur.left;
 7             if(mostRight != null){
 8                 while(mostRight.right != null && mostRight != cur){
 9                     mostRight = mostRight.right;
10                 }
11                 if(mostRight.right == null){
12                     mostRight.right = cur;
13                     cur = cur.left;
14                     continue;
15                 }else {//第二次达到 逆序打印左子树的右边界
16                     mostRight.right = null;
17                     printRightEdge(cur.left);
18                 }
19             }
20             cur = cur.right;
21         }
22         //最后退出循环之后，单独打印整棵树的右边界
23         printRightEdge(head);
24     }

Morris遍历的应用

如何判断一棵树是否是搜索二叉树？

中序遍历升序就是搜索二叉树。

 1     public static boolean isBST(TreeNode head){
 2         if(head == null) return true;
 3         TreeNode cur = head;
 4         TreeNode mostRight = null;
 5         int preValue = Integer.MIN_VALUE;//上一次得到的值
 6         while(cur != null){
 7             mostRight = cur.left;
 8             if(mostRight != null){
 9                 while(mostRight.right != null && mostRight != cur){
10                     mostRight = mostRight.right;
11                 }
12                 if(mostRight.right == null){
13                     mostRight.right = cur;
14                     cur = cur.left;
15                     continue;
16                 }else {
17                     mostRight.right = null;
18                 }
19             }
20             //中序遍历的操作时机在这里 所以在这里进行判断
21             if(cur.val <= preValue){//没有递增
22                 return false;
23             }
24             preValue = cur.val;
25             cur = cur.right;
26         }
27         return true;
28     }

总结

树型DP问题的套路：定义一个类收集树的信息，定义一个递归函数，递归地收集左子树的信息和右子树的信息，再整合得到以当前节点为根的树的信息。

什么时候用树型DP什么时候用Morris遍历？

当必须得到左树的信息和右树的信息后，再在当前节点整合二者信息后做出判断则用树型DP是最优解。

当不需要整合左树和右树信息的时候，可以用树型DP，但是Morris是最优解。

Tags: 数据结构和算法